Чтобы вызвать звук необходимо произвести колебания. Чтобы получить музыкальный звук необходимо, чтобы колебания имели постоянную частоту, т.е. стабильную высотность, которой исполнитель мог бы легко управлять. В электроинструментах стабильные и управляемые колебания получают с помощью электроники, у неэлектрических - за счет стоячих волн. Мы будем рассматривать колебания на примере струн, поскольку здесь они более наглядны, чем колебания воздуха в духовых инструментах, и менее сложны по сравнению с колебаниями дощечек и кожи ударных инструментов.
Натянутые струны скрипки, фортепиано и т.д. колеблются столь быстро, что разглядеть что-либо невозможно. Однако, можно провести несколько любопытных экспериментов, позволяющих понять работу струн с помощью нескольких метров гибкого резинового шланга. Садовый поливной шланг для этого недостаточно гибок, лучше всего взять резиновый шланг или длинную бельевую веревку. Привяжите или прижмите один конец шланга, а другой слегка натяните одной рукой (сильно натягивать не нужно, небольшой прогиб не страшен). Теперь другой рукой оттяните шланг в сторону, чтобы образовался выступ, и, отпустив его, вы увидите в замедленном темпе то, что происходит при щипке струны. Можно наблюдать, как выступ пробежит вдоль "струны" и вернется обратно. При возврате он толкнет Вашу руку, но если Вы держите "струну" крепко, произойдет новое отражение.
Первое, что Вы должны заметить, это то, что скорость движения волны по струне возрастает с увеличением ее натяжения. Это свойство используется при настройке инструментов, но сейчас мы не будем на этом останавливаться. Скорость движения волны зависит и от "веса" струны - в более толстой, тяжелой струне (при равной длине и натяжении) она будет медленнее, чем в легкой.
Теперь остановимся на отражении, которое происходит на закрепленном конце. Заметьте, что если оттягивать струну влево, то выступ побежит с левой стороны, но при возврате будет расположен справа - при отражении происходит инвертирование. Этот эффект наблюдается не только в струнах, но и в духовых и ударных. Волна инвертируется в момент, когда сталкивается с какой-либо неподвижной или трудно преодолимой преградой.
Несмотря на то, что струны музыкального инструмента закреплены с обоих концов, наблюдаемые процессы при щипке струны в них будут аналогичными. Сперва струна оттягивается в некой точке, а затем отпускается, как показано на рисунке. Если приглядеться, можно различить форму, которую образует бегущий выступ (показано тонкой линией на рисунках ниже), движущийся вдоль струны в обоих направлениях. Для наблюдений лучше использовать басовые струны, оттягивая их в нескольких миллиметрах от точки крепления. Фигура, образованная бегущим выступом, видна лучше, чем сама струна, потому что точку покоя, в которой происходит смена направлений, выступ проходит мгновенно, а к краям его движение замедляется.
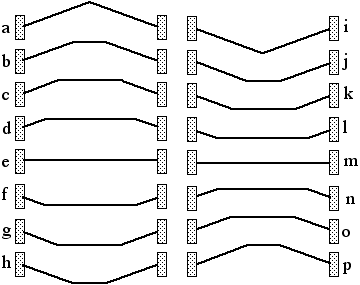
Схема движения выступа, образованного при щипке струны. Жирной линией показана сама струна, тонкой - фигура, образованная движением выступа. В фазах, отмеченных буквами (d) и (j), струна представляет прямую линию. В эти моменты потенциальная энергия ее колебаний исчерпана, а кинетическая энергия максимальна. Заметим, что в момент отражения положение выступа меняется на 180 градусов с верхнего на нижний или наоборот. Обратите внимание на проход выступов одного "сквозь" другой в момент, когда они встречаются посередине.
Схема, показывающая отражение движущихся выступов, при возбуждении струны смычком.
Отчего при отражении происходит инвертирование? Поскольку струна закреплена на неподвижном объекте, то и точка отражения является неподвижной. Теперь посмотрите на движение струны на левых рисунках, отражающих ее положение в разное время. Видно как часть струны позади выступа возвращается к своему первоначальному состоянию (на рисунках - вниз). Чем ближе выступ к концу струны, тем он становится меньше, и при его достижении он исчезает - в этот момент струна становится прямой. Однако движение струны вниз не прекращается, и, пройдя точку покоя, она образует обратный выступ, который начинает движение в обратном направлении.
Если раскачивать вверх-вниз незакрепленный конец струны, можно наблюдать один интересный эффект. С помощью резинового шланга можно проделать этот опыт самостоятельно. Если такой возможности у Вас нет, то взгляните на представленную ниже диаграмму.
Мы опять видим инвертирование отраженной волны, из-за чего после отражения мы получаем уже две волны (с одинаковой частотой и амплитудой), которые движутся в противоположных направлениях. В точке крепления струны, где они складываются, движение прекращается, т.е. имеет место нулевое перемещение, благодаря которому и возникает инвертированное отражение. Но если вы посмотрите на сплошную линию на диаграмме (представляющую собой результат суммирования двух волн), то увидите, что на струне есть и другие неподвижные точки. Эти равноудаленные друг от друга точки, играющие важнейшую роль в функционировании любого музыкального инструмента, называются "узлами" (node) вибрации. Посередине между узлами располагаются "пучности" (antinode) - зоны максимального движения. Обратите внимание, что эти выступающие зоны не движутся по струне. При сложении двух волн, бегущих в противоположных направлениях, образуется стоячая волна.
Две движущиеся волны при слиянии образуют стоячие волны.
Посмотрите на рисунок, который представляет последовательность фаз движения волн во времени (время течет сверху вниз). Синяя волна движется вправо, зеленая влево, красная волна является суммирующей и показывает, что происходит при столкновении двух волн (по научной терминологии - при наложении). Отмечены положения (узлы/nodes) в которых обе движущиеся волны нейтрализуют друг друга и другие зоны (пучности/antinodes), в которых происходит сложение волн, и колебания обладают максимальной амплитудой. Можно сказать, что приведенная выше диаграмма представляет колебание 5-й гармоники струны, длина которой равна ширине диаграммы. Здесь мы коснулись темы, которая будет освещена в следующей главе.
Гармоники и моды (типы) колебаний
На музыкальном инструменте струна закреплена с обоих концов, которые ограничивают возможные колебания и на которых во время колебаний расположены узлы. Струна, имеющая длину L, образует стоячую волну, длина которой равна удвоенной длине струны (длина волны = 2L), что демонстрируется на первом из рисунков следующей серии. При этом узлы расположены на концах струны, а пучность посередине между ними. Это одна из мод ("мода" - тип колебаний струны). Какие еще моды встречаются на струне, закрепленной с обоих концов? Ниже приводятся примеры таких стоячих волн.
Рисунки демонстрируют первые четыре моды колебаний идеальной* закрепленной струны (увеличено по вертикали).
В каком соотношении находятся моды колебаний? Частота колебаний волны равна отношению ее скорости к длине: f=v/длина волны. Таким образом, для струны длиной L, длины волн составят 2L, L, 2L/3, L/2, что можно записать так 2L/n, где n - номер гармоники.
Базовая частота или 1-я мода имеет частоту f1= v/длина волны = v/2L
Частота 2-й гармоники f2= v/l2 = 2v/2L = 2f1
Частота 3-й гармоники f3= v/l3 = 3v/2L = 3f1
Частота 4-й гармоники f4= v/l4 = 4v/2L = 4f1 ...
fn= v/ln = nv/2L = nf1
Все волны движутся по струне с одинаковой скоростью, поэтому волны с различными длинами имеют разные частоты, как показано на рисунках. Мода самой нижней частоты (f1) называется базовой. Частота n-ной моды будет в n раз больше базовой. Все эти моды (как и звуки, которые они образуют) называются гармониками струны. Частоты f, 2f, 3f, 4f и т.д. называется последовательностью гармоник. Музыканты хорошо знакомы с этими последовательностями, особенно те, кто играют на натуральных горнах или знакомы с флажолетами. Если для примера мы возьмем базовую частоту соответствующую ноте С3, т.е. альтовой До (частота = 131Гц), то ее гармоники будут иметь высотности, показанные на следующем рисунке. Высотность нот дана в приближении до четверти тона. При этом октавы являются чистыми, а вот другие интервалы не совсем соответствуют равномерно темперированному строю.
Нотное написание первых 12-ти гармоник (флажолетов) на примере ноты До. При прослушивании звукового файла (записанного в форматах au и wav) обратите внимание на высотность звуков.
Седьмая и одиннадцатая гармоники приходятся почти посередине между нотами равномерно темперированного строя, поэтому обозначены с половинками диезов.
Вы сами можете получить эти звуки на струнах. Проще это сделать на басовых струнах гитары, виолончели или контрабаса*. Для этого коснитесь слегка струны в точке, которая отстоит на длину =1/n от ее конца (где n = 1,2,3 и т.д.), а затем проведите смычком. Или слегка коснитесь струны в точке, которая приходится на длину =1/n от ее конца, ударьте по струне недалеко от подставки и мгновенно отдерните прижатый палец. Благодаря касанию, в точке произойдет образование узла, который образует моду, имеющую узел в данной точке. Вы легко сможете найти на струне от двух до шести флажолетов (если Вы только что проделали этот эксперимент, то, наверное, обратили внимание, на то, что двенадцатый лад, отвечающий за получение октавы, расположен менее, чем на половине длины струны, поэтому то место, где Вы касались струны для получения 2-й гармоники, находится не совсем точно над этим ладом).
* "Идеальной" я называю струну, которая, обладая абсолютной гибкостью, позволяет оттягивать ее без усилий в любом месте. Но поскольку реальные струны обладают жесткостью, их рабочая длина (которую мы обозначали в формулах буквой L) немного меньше физической длины, и это одна из причин, почему на басовых струнах применяется обмотка, а голая струна G (соль) классической гитары плохо строит в верхних позициях.
Упражнение для гитаристов
На настроенной гитаре струна В(си) и верхняя Е(ми) настроены примерно на 3-ю и 4-ю гармоники нижней струны Е(ми). Если взять на щипок басовую струну Е(ми) в любой точке кроме ее 1/3, струна В(си) начнет колебаться, возбуждаясь через колебания подставки от гармоники 1-й струны. Если взять на щипок басовую струну Е(ми) в любой точке кроме ее 1/4, отзовется верхняя струна Е(ми). Гитаристы обычно начинают настройку следующим образом: настраивают в унисон 4-ю гармонику басовой Е(ми), 3-ю у струны А(ля) и верхнюю струну Е(ми), затем струну В(си) строят по 3-й гармонике верхней Е(ми), а затем по 4-й гармонике А(ля) 3-ю гармонику струны D(ре). Настроить струну G(соль) по гармоникам не получится, в связи с невозможностью получения верхних гармоник, что связано с физическими параметрами толщины и жесткости самой струны, поэтому ее настраивают октавами, используя лады. По некоторым причинам (о которых будет сказано в конце главы), данный метод настройки достаточно приблизителен и требует дальнейшей подстройки при помощи ладов. Самой точной настройкой все-таки является компромиссная, которая осуществляется по аккордам, которые исполнитель собирается брать на грифе инструмента.
Гармоники (флажолеты) в музыке
Композиторы часто применяют гармоники/флажолеты на струнных инструментах, при этом наиболее часто используют "четвертую касательную". Одним пальцем музыкант зажимает струну, получая ноту за счет отрезка определенной длины, а другим легко касается струны там, где располагается нота на 4 тона выше (отсюда и название). Данная точка лежит на четверти длины отрезка струны, поэтому образуется 4-я гармоника базовой частоты в четыре раза больше базовой, т.е. получается интервал в две октавы. Струнные гармоники/флажолеты называются "натуральными" если они образованы от открытых струн и "искусственными" если струна прижимается. Ниже на рисунке показано, как берется натуральный флажолет. Для наглядности рисунок вытянут по вертикали.
Прослушайте фрагмент. Сначала звучит открытая струна А(ля), затем ее четвертая касательная (4-я гармоника).

Так обозначается на нотном стане "четвертая касательная" на скрипичной струне А(ля)
Немного технической информации для струнников
Несмотря на то, что "четвертая касательная" наиболее часто встречающийся флажолет, это не вполне удачный пример, поскольку получить четвертую гармонику гораздо проще, нежели "две четверки". Как известно, касание струны на отрезке 1/n (где n - целое число) дает n-ую гармонику, и для низких гармоник правило соблюдается, но для высших гармоник особое значение играет толщина струны, и здесь формула перестает работать. Таким образом, гармоники выше 8-й практически не берутся.
Если взять на струне подряд пять полутонов, то мы получим точку, соответствующую 1/3 длины струны, то есть "пятая касательная" даст нам третью гармонику. Гармоники расположены в следующем порядке:
| интервал на грифе | часть струны | номер гармоники | интервал от базовой ноты |
| октава | 1/2 | 2 | октава |
| квинта | 1/3 | 3 | октава + квинта (дуодецима) |
| кварта | 1/4 | 4 | две октавы |
| большая терция | 1/5 | 5 | 2 октавы + б. терция |
| малая терция | 1/6 | 6 | 2 октавы + квинта |
| ув. кварта | 2/7 | 7 | 2 октавы + м. секста повышенная |
| малая секста | 3/8 | 8 | 3 октавы |
| большая секунда | 1/9 | 9 | 3 октавы + б. секунда |
Положения нот звукоряда соответствуют чистому строю. Касание струны на 2/9 ее длины предпочтительней, чем на 1/9, хотя данная точка расположена не над нотой гаммы, а немного выше малой терции. Буду рад, если альтисты или виолончелисты исполняющие "Практикующая бесконечность" Радулески (Radulescu's "Practicing Infinity") пришлют мне свои предложения о способах исполнения высоких флажолетов.
Несовершенство настройки по гармоникам (флажолетам)
Есть несколько проблем при настройке любой гитары, в том числе при использовании флажолетов, о чем говорилось выше. Приблизительность настройки инструмента очевидно связана с равномерной темперацией. Даже если бы струны были идеальны, а положение ладов на грифе идеально отвечало равномерной темперации, при настройке по четвертой гармонике струн E-A (ми-ля), и A-D (ля-ре), октава между открытой нижней E(ми) и нотой ми на 2-м ладу струны D(ре) отклонялась бы приблизительно на 4 цента ((4/3)222/12=1.996), что приводило бы к появлению одного интерференционного биения в несколько секунд.
Другая проблема заключается в том, что в зоне верхнего порожка и подставки струны не могут обеспечить абсолютную гибкость (что было отмечено выше). В результате 1-й обертон на струне всегда будет чуть выше октавы, второй выше чем дуодецима (октава + квинта), и так далее. Так настройка в унисон 4-ой "гармоники" струны Е(ми) и 3-ей гармоники струны А(ля) при сравнении открытых струн даст интервал несколько больший, чем кварта, отчего приходится исправлять настройку, чтобы иметь равномерную темперацию.
Еще один отрицательный момент относится к расположению ладов и подставки. При прижиме струны на двенадцатом ладу увеличивается и ее длина (это уже не самое короткое расстояние между верхним порожком и подставкой), и ее натяжение. Вследствие этого, а также из-за выгиба конца струны, будь 12-й лад точно посередине между верхним порожком и подставкой, мы бы имели интервал больше октавы. Поэтому расстояние от подставки до 12-ого лада делают несколько большим, чем до верхнего порожка. Необходимо отметить, что в зависимости от вида струн эффект может быть различен. На электрогитарах есть возможность регулировать положение каждой подставки струны, на некоторых гитарах подставку поворачивают под углом, а в случае с классической гитарой прямая подставка ведет к определенному компромиссу в настройке.
Вышеописанные моменты сложно отследить с большой точностью, поскольку при анализе звука струны, возбуждаемой щипком, неточности составляют лишь несколько центов, что не намного больше разрешающей способности слуха или приборов настройки. Настройка колками также не позволяет достичь точности менее двух центов. С другой стороны, если Вам удастся интонировать мелодию с точностью в пределах двух центов, это будет большая удача - большинству музыкантов такое не по силам!
Определенная часть проблем настройки касается старения струн. Там, где Вы касаетесь их пальцами левой руки, они вбирают в себя пот и становятся более тяжелыми (хотя может иметь место и износ материала в местах, которые трутся об лады). Струны также изнашиваются под пальцами правой руки. Неоднородность струн ведет к невозможности их точной настройки. Мойка струн может помочь лишь отчасти.
Конечно, на безладовом инструменте большинство этих проблем можно обойти, но аккордная техника при этом сильно страдает.

На рисунке показаны гармоники открытой струны СОЛЬ контрабаса или виолончели. (Ноты для контрабаса записываются октавой выше его звучания.) Над нотами указаны номера гармоник, а под ними записаны приблизительные частоты в Герцах, причем для наглядности сделано округление чисел. Данный пример демонстрирует закон изменения высотности гармоник, и, хотя реальные частоты составляют пропорционально несколько меньшие значения, динамика возрастания частот от значения в 100Гц отражена абсолютно точно. (Приведенные значения частоты ноты СОЛЬ и ее гармоник могли бы иметь место при камертоне Ля=449Гц. Примечание переводчика).
Перепечатка статьи возможна только с согласия автора Джо Вулфи J.Wolfe()unsw.edu.au, а также фирмы ГОСПОДИН МУЗЫКАНТ®, осуществлявшей ее перевод.
